点击次数：

随着人工智能的发展，语音识别技术取得了长足的进步。其中，自监督预训练的语音模型因其强大的性能和鲁棒性，成为该领域的研究热点之一。然而，这些模型通常具有大量的参数，导致计算资源消耗巨大，限制了它们在许多实际应用场景中的使用。

本文介绍清华大学语音与音频技术实验室（SATLab）在信号处理领域旗舰期刊IEEE Journal of Selected Topics in Signal Processing (JSTSP)上预先出版的论文Unstructured Pruning and Low Rank Factorisation of Self-Supervised Pre-Trained Speech Models。这篇论文提出了一种对无监督预训练语音大模型进行压缩的新方法，通过结合非结构化剪枝和截断奇异值分解来实现硬件通用性好、压缩损失小的模型压缩，在语音识别任务上实现了大幅优于蒸馏和结构化剪枝基线方法的性能。

H. Wang and W.-Q. Zhang, “Unstructured pruning and low rank factorisation of self-supervised pre-trained speech models,” IEEE Journal of Selected Topics in Signal Processing, 2024. doi: 10.1109/JSTSP.2024.3433616.

背景：非结构化与结构化剪枝

以HuBERT、WavLM为代表的无监督语音预训练模型具有很强的表征能力和稳健性，仅需少量有标注数据微调就能在各类语音任务上取得良好的表现。不过，这类模型参数量通常较大，难以运行在各类算力受限的可移动设备上，这限制了它们在许多实际场景中的应用。因此，对这类语音预训练模型进行压缩有着重要的意义。

模型剪枝是语音预训练模型压缩的重要方法之一。通过移除网络中不重要的参数，模型剪枝可以削减网络的参数量，实现减少存储压力、加速计算的目的。根据剪枝的最小单元的不同，模型剪枝方法可以划分为非结构化剪枝和结构化剪枝。其中，非结构化剪枝以一个个单独的参数作为独立的剪枝单元，而结构化剪枝则以连续的参数组，例如矩阵的行或列为最小单元。

非结构化剪枝的自由度高，不容易“误伤”关键参数，因此有着更小的性能损失，但剪枝得到的是稀疏矩阵，为了实现稀疏矩阵的加速运算，一般需要特定的计算硬件或是计算库，使用起来有一定的困难；另一方面，结构化剪枝直接让矩阵变得更小，因此硬件适配性更好，不过性能损失通常更大。

为了兼顾硬件适配性和压缩模型的性能，这篇文章尝试通过截断的奇异值分解将非结构化稀疏的矩阵转换为更小的稠密矩阵，并且通过核范数正则化、可学习奇异值分解等方法实现了近乎无损的转换。

主要方法：结合剪枝和矩阵分解

非结构化剪枝得到的稀疏矩阵有可能具有低秩性。一些理论研究表明，矩阵的稀疏度会影响矩阵秩的上界。下图比较了HuBERT模型注意力层和线性层矩阵在剪枝前后奇异值排布的变化情况。可以看出，剪枝之后，稀疏矩阵的奇异值整体下降了。数学上的分析告诉我们，截断的奇异值分解会得到一对较小的稠密矩阵，而它们的乘积与原矩阵的误差则是被丢弃的奇异值之和。这也就是说，对稀疏矩阵进行截断的奇异值分解会有更小的重构误差， 因此对性能的影响也有可能更小。

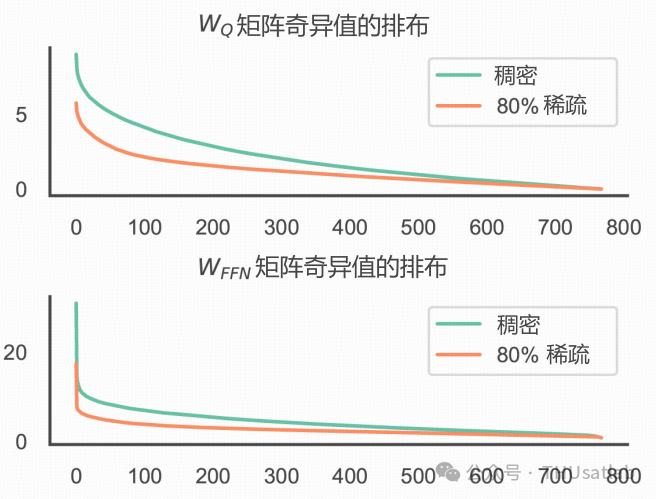
稀疏/稠密HuBERT模型中矩阵奇异值的排布

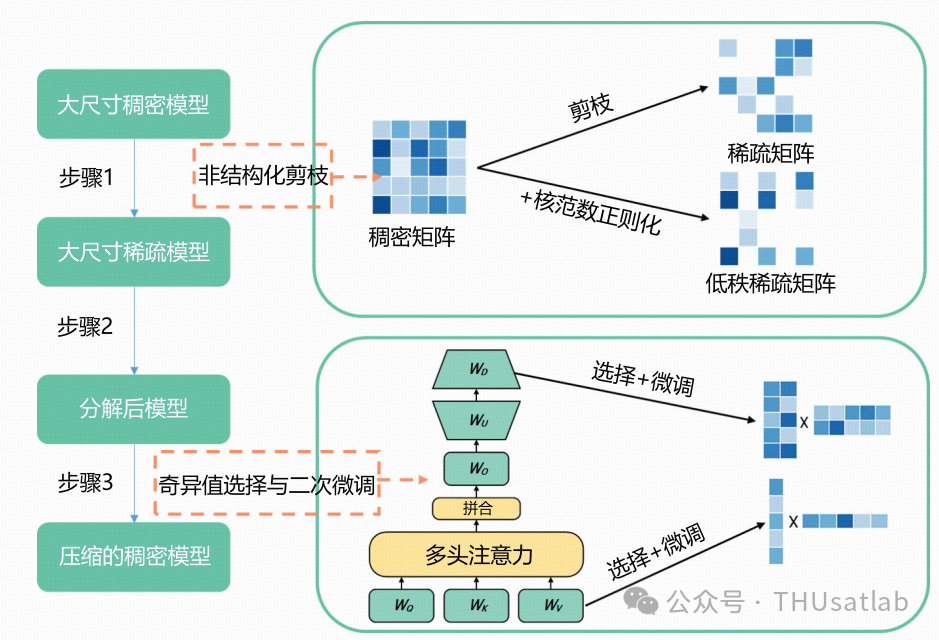
不过，低秩性并不是稀疏矩阵的必然属性，例如，对角矩阵是极其稀疏的，但同时也是满秩的。另外，非结构化剪枝模型中的一些矩阵可能是低秩的，但另一些矩阵可能并不是。因此，为了保证剪枝过程中低秩结构的存在，我们引入了核范数正则化来实现性能和低秩性之间的平衡；为了根据每个矩阵的秩选择最合适的SVD截断比例，我们设计了一种可学习的奇异值选择策略来学习每一层的最佳秩。我们提出的方法的概览如下所示：

文章方法的概览。此方法主要分三个步骤：（1）先通过非结构化剪枝得到稀疏模型（2）进行截断的奇异值分解（3）通过二次微调获得压缩的稠密模型。核范数正则化和可学习奇异值分解有助于更好地利用稀疏模型中潜在的低秩性

核范数正则化

核范数是矩阵秩的最优凸近似，定义为矩阵奇异值之和。我们观察到，在剪枝训练后期，随着模型的稀疏度逐渐稳定，识别率不断增强，模型的核范数在训练过程中呈现上升趋势。

如下图所示，在训练过程的末期，识别错误率随着网络逐渐从剪枝损失中恢复而开始下降，但其核范数在逐渐上升，表明这期间矩阵的秩也在逐渐提高。

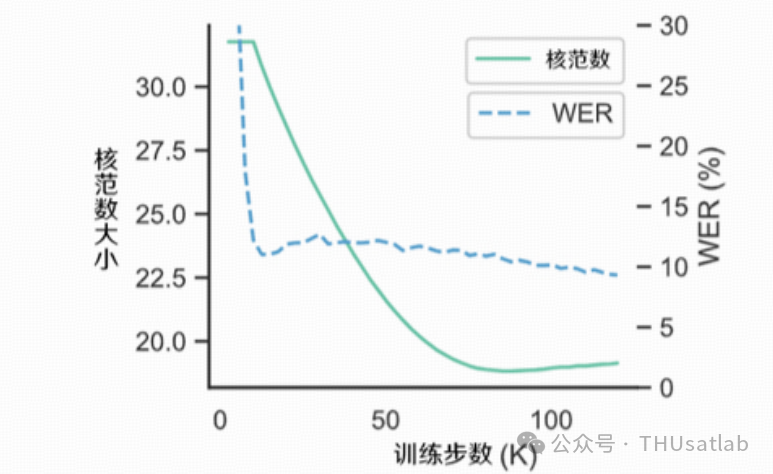
稀疏/稠密HuBERT模型中矩阵奇异值的排布

尽管充分训练得到的模型具有更好的性能，但其秩的上升会导致截断SVD的重构误差上升，这足以抵消充分训练带来的性能改善。因此，我们把矩阵的核范数作为一个额外的正则化项，通过限制矩阵的核范数保证模型能够学习到稀疏且低秩的结构。

除此之外，由于计算核范数涉及到对矩阵进行奇异值分解，计算的时间复杂度较大，因此我们采用了一种核范数的近似快速算法，计算复杂度由矩阵维度的三次方降低为二次方。

可学习的奇异值选择策略

在进行截断SVD时，为模型中的所有矩阵使用相同的截断比例可能并不是最合理的策略。由于语音预训练模型的层间差异，即使稀疏度相同，不同层的矩阵的秩也可能不同。更进一步地，对同一层的不同矩阵来说，前馈层的矩阵和注意力层的矩阵的秩也可能不同。

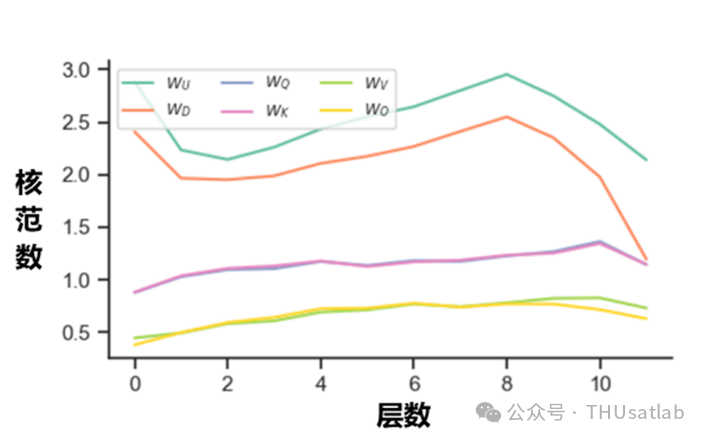
稀疏HuBERT模型中各层矩阵的奇异值

上图展示了稀疏HuBERT模型中核范数随层数的分布情况。可以看到，各个稀疏矩阵的核范数在层中的分布并不均匀，代表其秩同样可能具有较大差异。例如，对网络中FFN层的矩阵来说，最顶层的秩就比最靠近输入的最底层要低很多。

为解决这一问题，我们为网络中每个矩阵的每个特征值单独设计了一个剪枝掩码，通过额外加入的L0正则化项来优化这些掩码，从而学习到每个矩阵的最优奇异值移除比例。

实验结果概览

我们在四类不同任务上对提出方法的效果进行了测试。下表比较了在语音识别、关键词检测、意图识别和说话人日志化四类任务上本文提出的稀疏+分解方法相比未经压缩的原始模型和非结构化剪枝模型的表现。

提出的方法在语音识别（ASR）任务上的表现

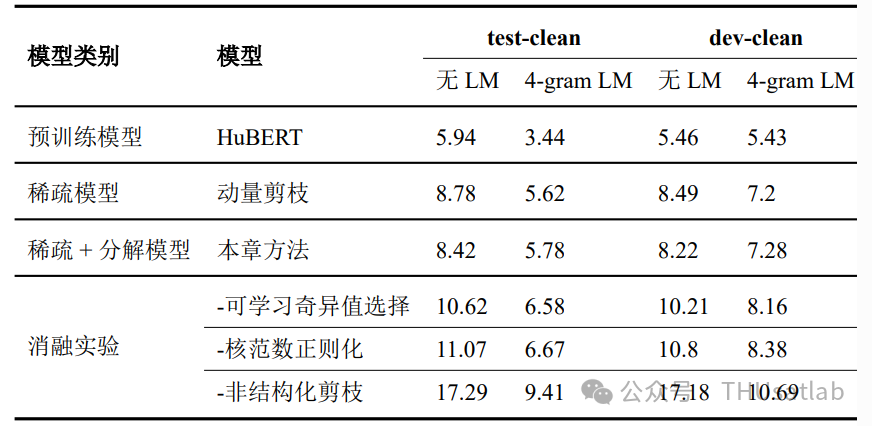
提出的方法在关键词检测（KWS）、意图识别（IC）和说话人日志化（SD）任务上的表现

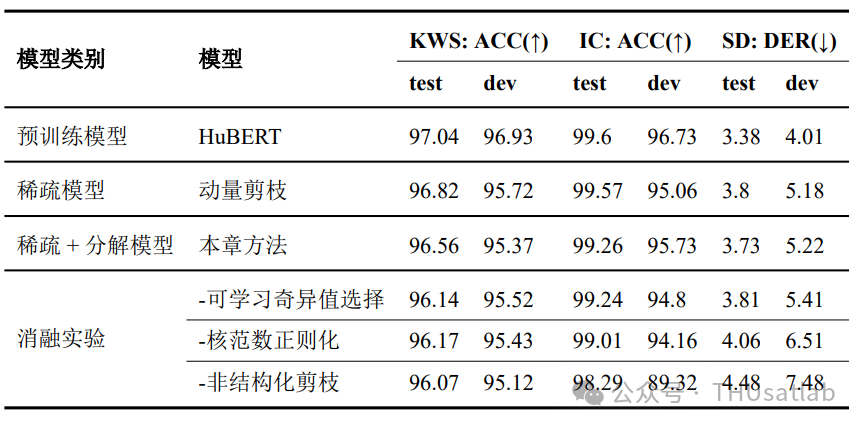
表格中稀疏模型80%的参数量被移除，而分解的模型保留了10%的奇异值，两者的非零参数量是相近的。

可以看出，文章提出的结合非结构化剪枝和矩阵分解的压缩方法在所有任务上都达到了接近或超过非结构化稀疏模型的性能，证明了这一方法可以几乎无损地将非结构化稀疏模型转换为硬件友好的压缩稠密模型。更进一步的消融实验表明，不使用可学习的奇异值选择策略或核范数正则化均会导致明显的性能下降，这表明了这两种策略的有效性。

与蒸馏和剪枝基线模型的对比

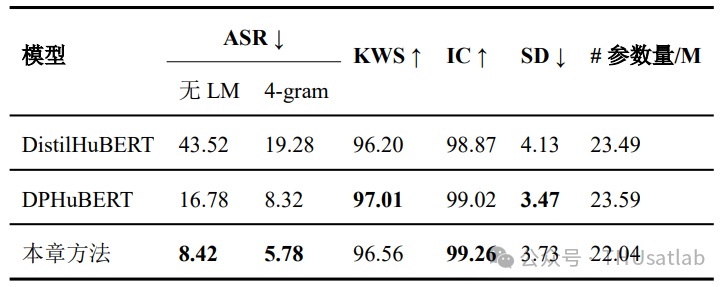
我们进一步对比了提出的方法和蒸馏模型DistilHuBERT、结构化剪枝模型DPHuBERT在ASR任务上的性能，选择的基线模型都具有较好的硬件适配性。

相比KWS等任务，ASR任务更加复杂，对压缩损失也更为敏感，因此直接进行知识蒸馏或结构化剪枝可能带来更大的性能损失，而提出的方法从压缩损失更小的非结构化剪枝模型出发，利用截断的奇异值分解进行几乎无损的非结构化到结构化的转换，从而更好地保留了未经压缩的原始模型的语音识别性能。

结束语

这篇文章关注到非结构化稀疏模型的低秩特性，并提出使用截断的奇异值分解将之转换为参数量更少的稠密模型。通过可学习的奇异值选择策略和核范数正则化方法，我们可在几乎不产生性能损失的情况下实现这一转换，兼顾了压缩模型的性能与硬件通用性。